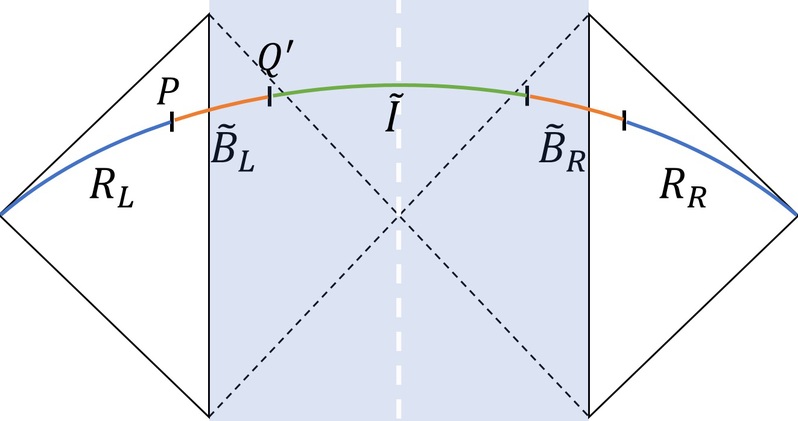
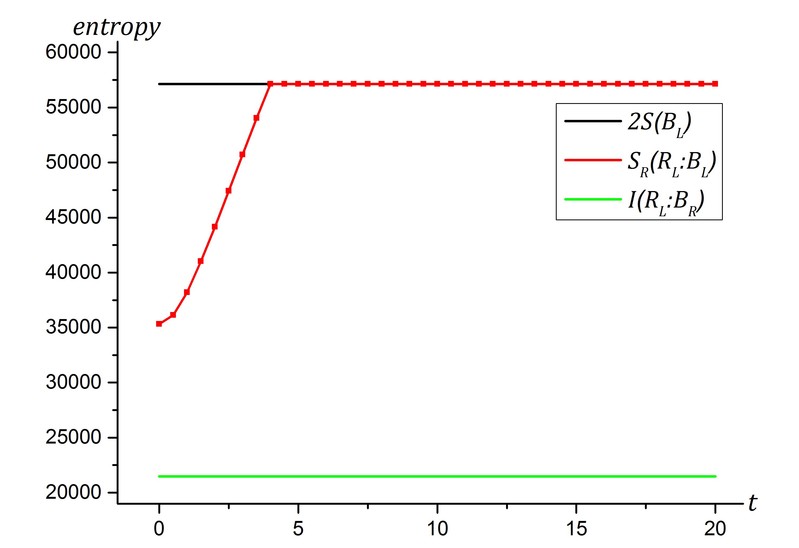
近日，复旦大学物理学系周洋课题组运用理论计算的手段，研究了黑洞蒸发过程中反射熵的变化，首次提出了反射熵的量子极值截面公式。该项研究成果于近期在线发表于Journal of High Energy Physics，https://link.springer.com/article/10.1007/JHEP11(2020)155

一个由初始量子纯态坍缩而成的黑洞由于其不断蒸发，使得辐射的冯诺依曼熵愈来愈大，甚至将超过黑洞热力学熵这一上限，从而导致著名的信息悖论。为了解决这一悖论，研究者们提出辐射的冯诺依曼熵在一定时间后应转而下降，形成所谓的“佩奇曲线”，这一时间拐点被称为“佩奇时间”。为了得到佩奇曲线，需要使用引力修正的公式来计算辐射的冯诺依曼熵，即“量子极值面公式”。该公式告诉我们，在佩奇时间之后，黑洞内部的一部分称为岛屿的区域贡献辐射的冯诺依曼熵，因而使其越来越小，符合佩奇曲线。

由于冯诺依曼熵仅在纯态黑洞体系能刻画黑洞与辐射的纠缠，当黑洞和辐射体系为混态时，找出类似的公式并解决信息悖论成为一个重要问题。为此，周洋课题组将适用于混态的关联度量——反射熵推广到引力系统，提出“量子极值截面公式”。利用该公式得到了反射熵的佩奇曲线，从熵的角度初步解决了混态黑洞体系的信息悖论。

此研究利用三种不同的黑洞蒸发模型计算反射熵，得到一致的结果。包括简单虫洞模型，世界尽头膜模型和永恒双黑洞与共形场论结合模型。周洋课题组在提出与量子极值面公式类似的量子极值截面公式后，在永恒双黑洞与共形场论结合的模型中计算了黑洞-黑洞、黑洞-辐射和辐射-辐射等之间的反射熵。发现黑洞-辐射反射熵满足佩奇曲线。此外，还得到黑洞-黑洞反射熵随时间逐渐减少至零、辐射-辐射反射熵逐渐增加至有限值等结果。

注：永恒双黑洞与共形场论模型

注：永恒双黑洞与共形场论模型中一侧黑洞与辐射之间的反射熵（红色），满足佩奇曲线

本研究为我们从熵的角度理解黑洞信息悖论提供了更多启发，并且揭示了近期科学家提出的黑洞孤岛的更多信息论特征。

该工作由我系周洋课题组独立完成。工作获得了国家自然科学基金的支持。论文的通讯作者为周洋，其他两名作者为课题组学生朱津纬和李添翼。

原文链接：https://link.springer.com/article/10.1007/JHEP11(2020)155