近日,复旦大学物理学系安正华团队,在《自然·物理》(Nature Physics)杂志上发表了其在非厄米磁子系统上的谱拓扑研究进展。该研究利用合成维度的概念,构建了一个高度调谐的基于微波光子-磁子耦合的非厄米散射系统,首次实现了磁子体系的非厄米谱拓扑,即本征谱的非平庸编织。论文以“Braiding reflectionless states in non-Hermitian magnonics”为题,于2024年11月1日在线发表,阐述了这一研究成果。 对能带的拓扑分类一直是能带理论中的关键,因为其对预测材料是否具有拓扑保护有着重要作用。而在能带理论中引入非厄米性后,对于非厄米能带的拓扑分类也更加复杂,因为在非厄米系统中存在着奇异点(EP)和点隙(Point-gap)的新概念。在非厄米系统中,通过环绕EP,两个或多个非厄米能带中会发生缠绕编织,形成不同的拓扑辫状结构,这些辫状结构可以用辫群来分类。 目前关于非厄米能带编织的一些工作的主要研究的都是非厄米系统中的共振态,然而在散射系统中还存在散射态的概念,并存在各种奇异性散射行为,如散射零点、完美吸收、连续体中的束缚态(BIC)等。一方面,这些散射行为的理论与预测无法只依靠共振哈密顿量;另一方面,对于非厄米散射系统中的散射态的编织研究还处于空白,而其相比共振态有着更大的实验自由度。 研究团队提出了一种等效哈密顿量,即散射哈密顿量,区别于对应于散射极点的共振哈密顿量,散射哈密顿量的本征值对应于其它散射奇异点,如零反射、零透射等。将散射哈密顿量应用于图1中的单端口微波散射系统,其本征值描述的是系统的无反射态(Reflectionless states,或称反射零点Reflection-zero)。在散射哈密顿量理论的指导下,通过调谐从源处注入系统的“辐射增益”与损耗的平衡,作者不仅可以调控散射哈密顿量本征值落在复频面实轴上的无反射模式,也可以在不引入实际增益的情况下实现PT对称保护的无反射模式,这与共振哈密顿量的PT对称不同,后者需要额外的增益使得极点落在实轴上。同时,通过散射哈密顿量理论,落在复平面的BIC点被证明是共振哈密顿量本征值与散射哈密顿量本征值的简并点,c-BIC与BIC性质类似,在散射谱中不具直接的可见性。总之,散射哈密顿量这一理论厘清了奇异性散射性质与哈密顿量之间的紧密联系。 图1:两类哈密顿量的实验展示。共振哈密顿量对应于散射极点,散射哈密顿量对应于散射零点。 与之前报道的关于编织的工作不同,研究团队同时研究了散射哈密顿量和共振哈密顿量的EP在参数空间中的演化行为,并在参数空间中规划出不同种类的参数路径,从实验上展示了非厄米磁子系统的两类能谱拓扑编织,分别表示散射态和共振态的编织,文章还揭示了散射态编织和共振态编织存在手性相反的关系。如图2所示,不同的编织结构可以用二阶辫群的群元来分类。 图2:通过在参数空间中选择合适的路径环绕EP,展示二阶辫群的不同群元,即不同的编织行为生成不同的辫状结构。(b-d)表示本征能谱的缠绕编织次数从0到2,从拓扑平庸的编织到拓扑非平庸的编织。 在这项研究中,研究团队不仅揭示了散射哈密顿量理论发挥着和共振哈密顿量同等重要的作用,也展示出了非厄米磁子系统在研究非厄米拓扑学中的重要意义,对于开发基于磁子的应用平台,包括拓扑能量传递、可调吸收器和逻辑电路等有着指导意义,还为通用的波调控器件设计和性能改进提供了具体思路。 论文的主要共同第一作者是复旦大学物理学系的博士生饶泽金和孟昌昊,通讯作者为复旦大学物理学系的安正华研究员,合作者包括物理系丁鲲研究员。该项目得到了国家自然科学基金委、上海市科学技术委员会、应用表面物理国家重点实验室、中德科学基金研究交流中心等的资助和支持。 论文地址:https://www.nature.com/articles/s41567-024-02667-x一、导读
二、研究背景
三、研究亮点
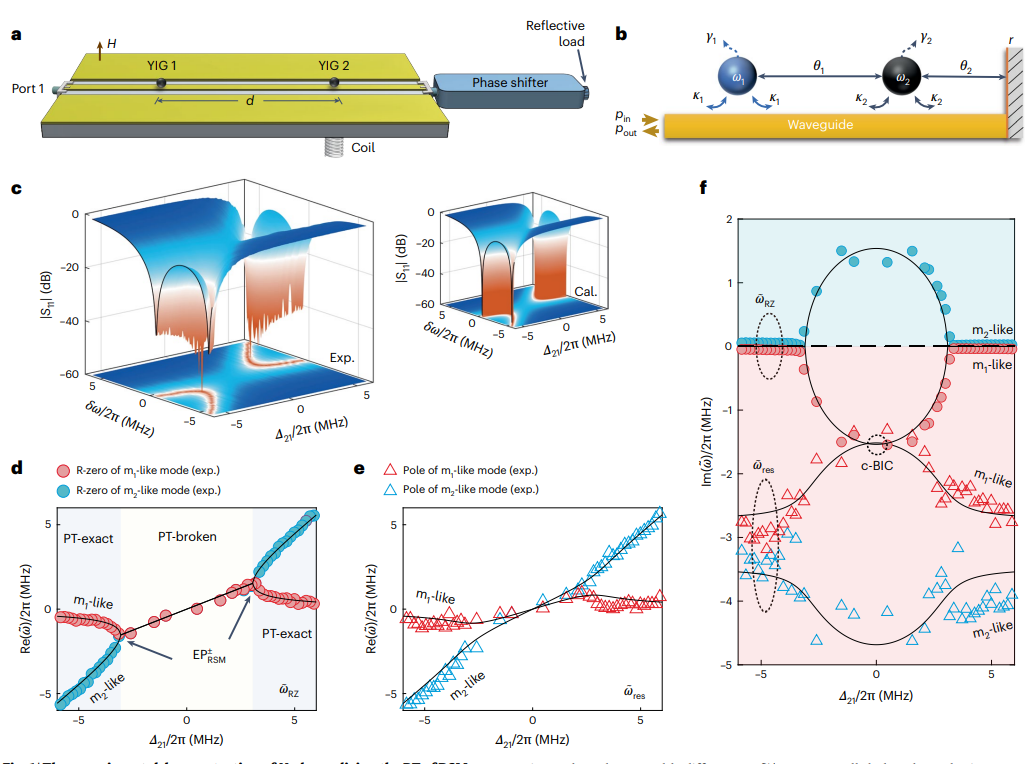
四、总结与展望