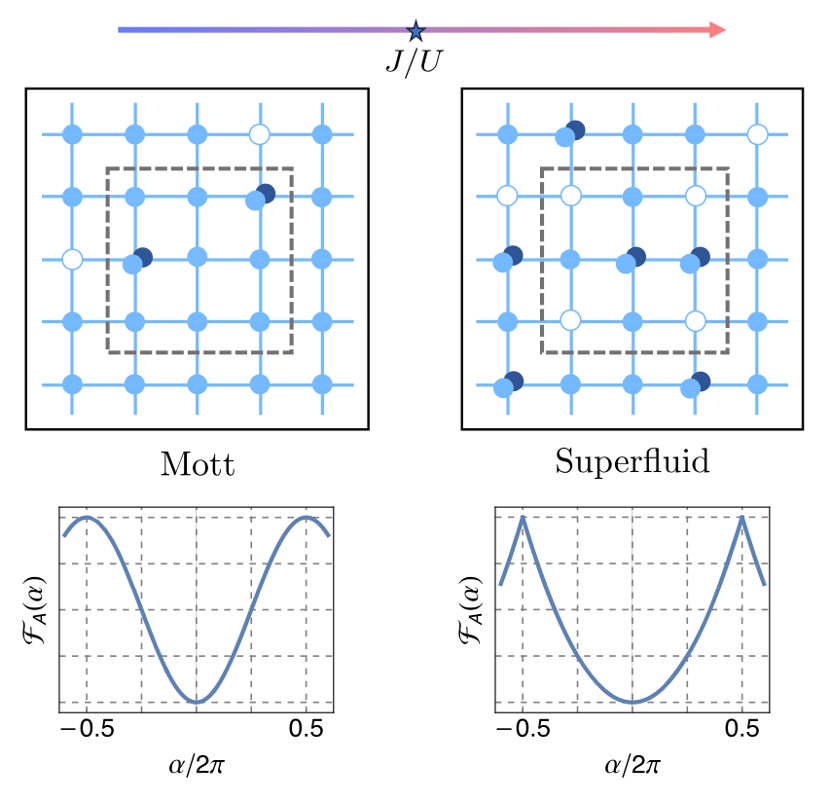
在量子系统中，每次测量都会导致波函数根据测量算符的本征态发生概率塌缩。因此，任何观测量的精确测量需要通过对大量独立实验结果的平均来实现。这些实验结果不仅提供了该观测量的期望值，还包含了量子系统中物理量内在涨落的信息。这些涨落反映了量子系统中的纠缠与关联，揭示了系统的微观结构及其动态行为。全计数统计（Full Counting Statistics, FCS）提供了一种系统化的方法来量化这些涨落。例如，在准一维电子系统中，全计数统计揭示了电荷的量子化，受到了广泛关注。近年来，FCS逐渐被应用于凝聚态物理的各个领域，包括量子相变、拓扑相及测量诱导相变等。

在近期的工作中，张鹏飞与清华大学高等研究院的合作者王昌言、周天罡、周伊能共同提出利用全计数统计中的尖点奇异性来区分有序相与无序相的方案。这项研究以玻色-哈伯德模型中的超流态到莫特绝缘态的量子相变为例，结合解析理论与数值模拟，揭示了当子系统的大小足够大时，FCS在超流相中作为相位角的函数会表现出明显的尖点奇异性，而在莫特相中则是光滑的。这种奇异性的出现被解释为不同半经典的涡旋构型之间的一阶相变。该研究的理论预言不仅丰富了我们对量子相变的理解，也为超冷原子系统和超导量子比特平台上的相关实验提供了新的方案。

图1：Mott绝缘体相与超流体相中全计数统计行为对比。

相关成果于2024年8月19日以“Distinguishing Quantum Phases through Cusps in Full Counting Statistics”为题发表于《物理评论快报》[Physical Review Letters 133, 083402 (2024)]。复旦大学物理学系张鹏飞青年研究员为通讯作者。研究得到了国家自然科学基金委(12374477)的支持。